Signal vs spectre
EN | FR
Dans la vie de tous les jours, les sons sont captés par notre appareil auditif et analysés par notre cerveau. Cependant, afin de mieux comprendre les phénomènes physiques découlant du son, on a recours à des méthodes d'analyse analogiques et numériques, qui utilisent différents types de représentation de la vibration sonore.
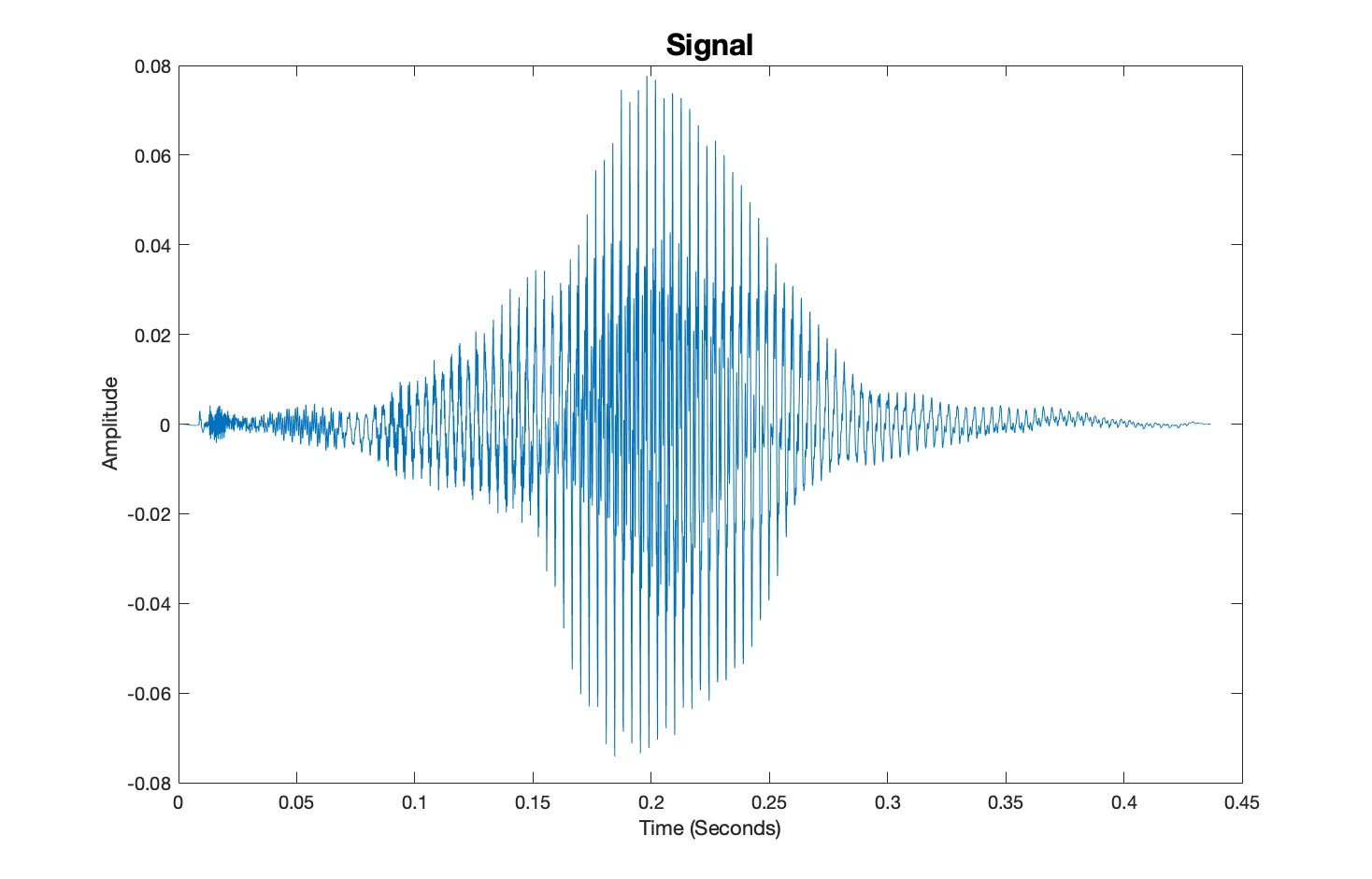
En premier lieu, l'onde sonore peut être représentée sous forme de signal. Il s'agit d'une représentation temporelle, où le temps (en secondes) constitue la variable indépendante. La variable dépendante, qui varie en fonction du temps, est l'amplitude de l’onde. S'il y a une captation sonore par un microphone, le signal peut être représenté sous forme d'une variation de tension, exprimée en Volts (V), telle qu’observée sur un oscilloscope. Il peut également être exprimé en termes de puissance électrique en Watts (W). Lorsque la vibration est convertie en signal numérique, son amplitude est représentée sur une échelle linéaire, comprise habituellement entre -1 et +1. C’est généralement ce que l’on visualise dans un logiciel d’édition ou de mixage audio. Le signal peut aussi être représenté par son niveau d’intensité ou niveau de pression acoustique en décibels (dB), toujours en fonction du temps. Pour les sons instrumentaux, on aura souvent recours au concept d'enveloppe temporelle, qui suit le même type de représentation.
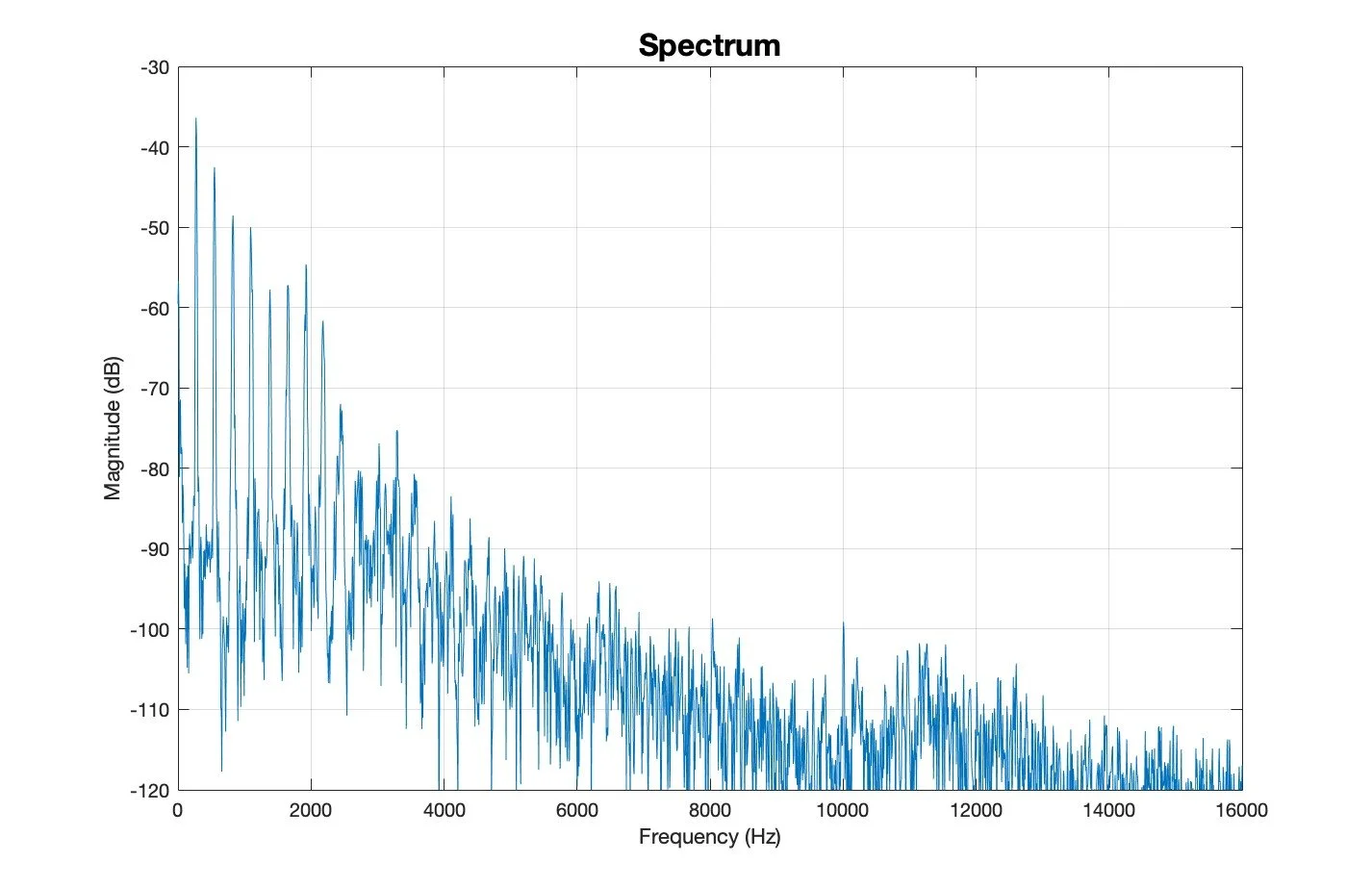
Ensuite, il est possible d'effectuer une opération mathématique sur le signal afin d'en obtenir une représentation fréquentielle. Cette opération s'appelle la "transformation de Fourier", et la représentation du son qui en résulte (la “transformée de Fourier”) est le spectre. Autrement dit, on obtient une représentation spectrale, où la fréquence en Hertz (Hz) est la variable indépendante et la magnitude du spectre, généralement exprimée en décibels ( dB), la variable dépendante. Si le spectre est harmonique, chacun des partiels apparaîtra à intervalles réguliers (en Hz) sur le graphique correspondant à ce type de représentation. En effet, les partiels d’un spectre harmonique se situent à des fréquences qui sont des multiples entiers de la fréquence dite fondamentale.
C'est à partir de ces deux principaux types de représentation du son (signal et spectre) qu'il est possible d'effectuer plusieurs mesures statistiques sur le son, appelées "descripteurs acoustiques".
Signal (représentation temporelle) d'un ton court de flûte (voir ci-dessous). Les valeurs d'amplitude représentées numériquement sont affichées sur une échelle linéaire et relative (de -1 à +1), c'est pourquoi elles n'ont pas d'unité.
Spectre d'amplitude (représentation de fréquence) du même son de flûte courte. Remarquez l'harmonie des partiels (rayures verticales bien définies et équidistantes à gauche) et la présence de bruit (en dessous des rayures et à droite) dans le son de flûte.